Exploring The Geometry Of Cones: A Comprehensive Guide

Exploring the Geometry of Cones: A Comprehensive Guide

Related Articles: Exploring the Geometry of Cones: A Comprehensive Guide

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Exploring the Geometry of Cones: A Comprehensive Guide. Let’s weave interesting information and offer fresh perspectives to the readers.

Exploring the Geometry of Cones: A Comprehensive Guide

The cone, a fundamental geometric shape, stands as a testament to the elegance and power of mathematics. Its simple form, defined by a circular base and a single apex, belies a rich tapestry of geometric relationships and applications. Understanding the shapes that contribute to the construction of a cone provides a deeper appreciation for its versatility and importance in various fields, from engineering and architecture to art and design.

The Building Blocks of a Cone:

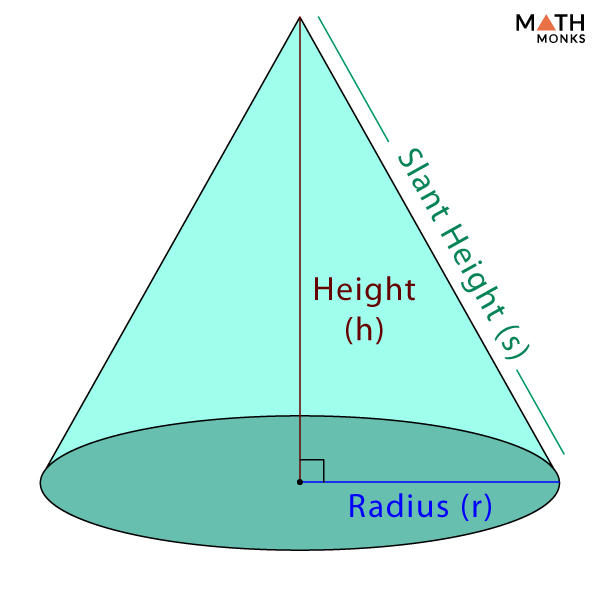
At its core, a cone is formed by the rotation of a right triangle around one of its legs. This process, known as revolution, results in a three-dimensional shape characterized by its circular base and its apex, the point opposite the base. The leg of the right triangle that coincides with the axis of rotation becomes the cone’s height, while the other leg forms the radius of the circular base.

Shapes That Form the Cone:

1. The Right Triangle: As mentioned, the right triangle is the fundamental shape that generates a cone. Its unique combination of a right angle and two legs, one of which becomes the cone’s height and the other its base radius, is crucial to the cone’s formation. The hypotenuse of the right triangle, when rotated, forms the slant height of the cone, a key element in determining its surface area and volume.

2. The Circle: The circular base of a cone is a direct result of the rotation of one of the legs of the right triangle. This circle defines the cone’s footprint and serves as the foundation for its volume and surface area calculations.

3. The Slant Height: The slant height, represented by the hypotenuse of the generating right triangle, connects the apex of the cone to a point on the circumference of the base. It plays a crucial role in determining the surface area of the cone, acting as the radius of the cone’s lateral surface.

4. The Apex: The apex, the point opposite the base, is the culmination of the rotating line segment that forms the cone’s slant height. It is a singular point that defines the cone’s height and acts as a focal point for its geometry.

The Importance of Understanding Cone Construction:

The ability to visualize and comprehend the shapes that contribute to a cone’s formation is essential for various reasons:

• Geometric Calculations: Understanding the relationship between the right triangle, the circle, and the slant height allows for accurate calculation of the cone’s surface area and volume. These calculations are fundamental in engineering, architecture, and other fields where precise measurements are crucial.

• Applications in Engineering and Design: Cones find applications in various engineering disciplines. From conical tanks and funnels used in fluid mechanics to conical bearings used in mechanical systems, understanding cone construction enables efficient design and optimization.

• Artistic and Architectural Expression: Cones are prevalent in art and architecture, from the iconic pyramids of ancient Egypt to the modern architecture of Frank Lloyd Wright. Understanding cone geometry allows artists and architects to manipulate its form for aesthetic and structural purposes.

FAQs about Cone Construction:

• Q: Can any triangle be used to generate a cone?

  • A: No, only a right triangle can be used to generate a cone. The right angle ensures that the rotating leg forms a circle, while the other leg defines the cone’s height and base radius.

• Q: What happens if the right triangle is rotated around its hypotenuse?

  • A: Rotating the right triangle around its hypotenuse results in a different three-dimensional shape, known as a sphere. This highlights the importance of the chosen axis of rotation in determining the resulting shape.

• Q: Can a cone have a square base?

  • A: No, a cone’s base must be circular. This is due to the fact that the cone is formed by the rotation of a right triangle, which inherently creates a circular base.

• Q: What are some real-world examples of cones?

  • A: Cones are ubiquitous in our world, from ice cream cones and traffic cones to the shape of a volcano and the pointed tip of a pencil.

Tips for Understanding Cone Construction:

• Visualize the Rotation: Imagine the right triangle rotating around one of its legs. This mental exercise helps to understand how the circle and the slant height are formed.

• Draw Diagrams: Use diagrams to represent the right triangle, the circular base, and the slant height. This visual representation aids in comprehending the relationships between the shapes.

• Experiment with Models: Build a physical model of a cone using paper or cardboard. This hands-on experience provides a tangible understanding of cone construction.

Conclusion:

The cone, a seemingly simple geometric shape, reveals a fascinating world of interconnected shapes and applications. Understanding its construction, from the right triangle that forms its foundation to the circular base and the slant height that define its geometry, provides a deeper appreciation for its versatility and importance in various fields. By exploring the shapes that make a cone, we gain a deeper understanding of the fundamental principles of geometry and its profound impact on our world.

Closure

Thus, we hope this article has provided valuable insights into Exploring the Geometry of Cones: A Comprehensive Guide. We hope you find this article informative and beneficial. See you in our next article!